
Llega un momento en la vida en el que quieres poner en orden las cosas y al mismo tiempo disponer de un acceso simple para soluciones complejas. Por ejemplo, quizás tengas varios scripts que se encargan de diferentes cuestiones (como encender y apagar un calentador, tomar fotografías con tus cámaras de seguridad, gestionar la detección de presencia, etc.), pero eres el único que puedes administrar estos scripts porque requieren de un mantenimiento a través de SSH, o a través de alguna página web obsoleta. Yo también he llegado a ese momento en mi vida y tengo que buscar una solución "global" que me permita administrar todas mis automatizaciones privadas y que ofrezca un fácil acceso para mi familia.
Estaba pensando en crear un panel de control web que se ajustara a mis necesidades, pero detesto el desarrollo web. Soy un poco vago y mis sitios no son para nada atractivos. Además, necesitaba que funcionara en todo tipo de dispositivos y tamaños de pantalla, y que también estuviera preparado para el futuro. Afortunadamente, pasé el suficiente tiempo buscando hasta que encontre la solución perfecta: Home Assistant (http://bit.ly/2hlOPOE) - HA para abreviar.
Home Assistant es una plataforma de domótica de código abierto desarrollada en Python 3 que soporta más de 650 componentes, que son módulos que facilitan la interacción con diversas cosas como switches físicos "inteligentes", relés, luces, sensores, dispositivos de red (televisores, routers y cámaras), software (como Kodi, MPD y Transmisión), servicios de red (como el tiempo), pero también permite agregar tus propios componentes personalizados. Las principales marcas y tecnologías de automatización del hogar, como Hue, Nest, IKEA, Vera, ZigBee y MQTT están presentes, puedes encontrar una lista completa de los componentes en http://bit.ly/2sWJsPy.
Además de los componentes, la plataforma cuenta con una interfaz web muy similar a un cuadro de mandos y un motor de automatización donde puedes combinar datos de diferentes componentes y generar un evento. Por ejemplo, si de lunes a viernes entre las 8:00 y las 15:00 el tiempo esta soleado, la temperatura exterior supera la 30 °C, no hay probabilidad de lluvia, y los aspersores de fuera han estado apagados durante al menos 4 horas, entonces activaremos los aspersores unos 20 minutos. Lo complicado de esta automatización es disponer de una forma de encender y apagar los aspersores; el resto lo proporciona los componentes y el motor de automatización de Home Assistant. Otros posibles usos pueden ser bloquear y desbloquear la puerta de entrada cuando una persona específica se conecte a la red wifi (aunque yo no lo haría personalmente) o iniciar el aire acondicionado automáticamente cuando el sistema detecte que estás llegando a casa del trabajo. Tienes más ejemplos en el video de 1 hora en http://bit.ly/2t0GgCI. Si estás familiarizado con Tasker para Android o IFTTT, Home Assistant es el equivalente para tu hogar.
Instalación
Puede instalar Home Assistant en cualquier dispositivo ODROID. Dependiendo de la cantidad de automatizaciones que tengas pensado tener, puedes usar un C1 para una configuración liviana, o incluso un XU4 para casas más grandes y reglas más complejas que pueden incluir el reconocimiento facial. Yo lo estoy usando en un C2 que funciona como reproductor Kodi sin problema.
Vamos a hacer una instalación "virtualenv", lo cual significa que todos los módulos necesarios de python se instalarán en un directorio específico y no interferirán con los módulos del sistema. Además utilizaremos un usuario distinto para Home Assistant. También hay imágenes Docker disponibles. Todas las instrucciones con comentarios están disponibles en http://bit.ly/2t0iaYC.
$ sudo apt-get update $ sudo apt-get dist-upgrade $ sudo apt-get install python-pip python3-dev $ sudo pip install --upgrade virtualenv $ sudo adduser --system homeassistant $ sudo addgroup homeassistant $ sudo usermod -G dialout -a homeassistant $ sudo mkdir /srv/homeassistant $ sudo chown homeassistant:homeassistant /srv/homeassistant $ sudo su -s /bin/bash homeassistant $ virtualenv -p python3 /srv/homeassistant $ source /srv/homeassistant/bin/activate (homeassistant)$ pip3 install --upgrade homeassistant $ exitPara iniciar y administrar el proceso, es mejor crear un servicio systemd para gestionarlo:
$ sudo vi /etc/systemd/system/homeassistant.service [Unit] Description=Home Assistant After=network.target time-sync.target Requires=time-sync.target [Service] Type=simple User=%i ExecStart=/srv/homeassistant/bin/hass -c "/home/homeassistant/.homeassistant" [Install] WantedBy=multi-user.targetPara iniciar Home Assistant, simplemente inicia su servicio:
$ sudo service homeassistant start $ sudo service homeassistant enableTen en cuenta que, si vas a utilizar componentes que necesitan HTTPS, deberás tener la hora configurada correctamente en el arranque, para que los certificados sean válidos. El inicio del servicio depende de systemd-timesyncd, que a su vez depende de que ntp *no* esté instalado:
$ sudo apt-get remove ntp $ sudo service systemd-timesyncd restart $ sudo systemctl enable systemd-timesyncdEn caso de tener problemas, podrás revisar los registros log a través de journalctl:
$ sudo journalctl -u homeassistant -fUna vez que se inicie el proceso, podrás conectarte a http://ip-odroid:8123/. Ten en cuenta que el primer arranque (o un inicio después de una actualización) puede ser algo más lento, así que déjelo trabajar durante unos minutos hasta que accedas a la interfaz web. Home Assistant cuenta con una aplicación nativa para IOS (http://apple.co/2tYi2WI), mientras que para los clientes de Android puedes configurar la página de HA como página de inicio (Chrome -> navega a http://ip-odroid: 8123 - > Menu -> Add to homescreen).
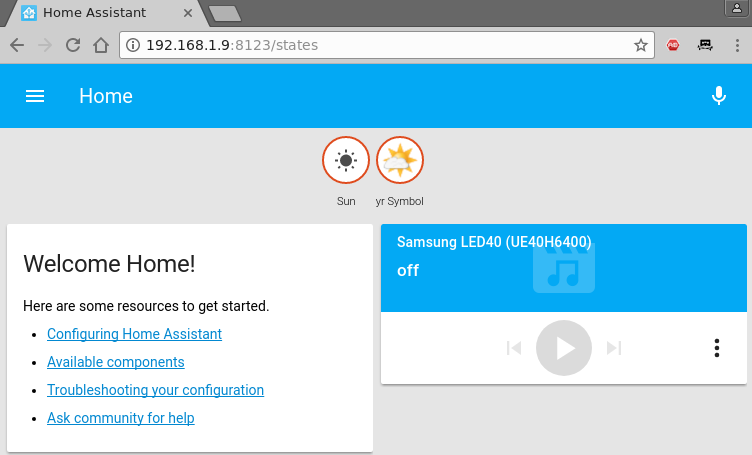
El archivo de configuración
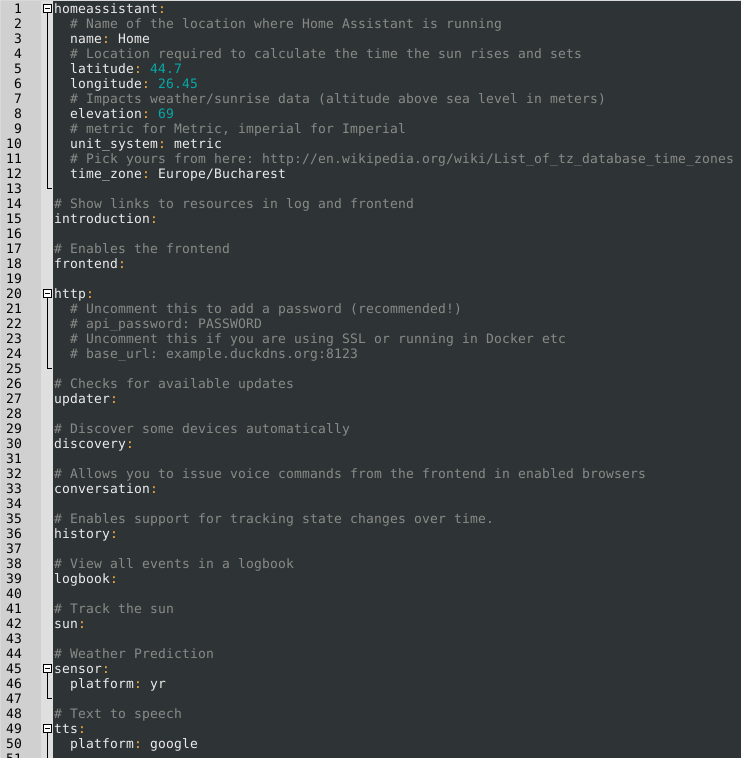
Iara poner en marcha los componentes y configurar tu instalación, tendrás que trabajar bastante con los archivos de configuración de Home Assistant. Es de esperar que, en una versión futura, puedas modificar la configuración directamente desde la interfaz web, pero por ahora, necesitarás un editor de texto. El archivo principal es /home/homeassistant/.homeassistant/configuration.yaml. Su formato es YAML, que significa "Yet Another Markup Language". Al igual que Python, usa espacios en blanco (¡no tabulaciones!) para delimitar las secciones de código. Por defecto, utiliza una sangría de dos espacios para las secciones anidadas. En el caso de que haya problemas, recibirás mensajes de error al iniciar el servicio. Puede validar la sintaxis con un servicio como http://www.yamllint.com/ que te permitirá saber dónde están exactamente los errores. También tienes una guía de solución de problemas en http://bit.ly/2tDHMsa.
Una vez que hayas realizado los cambios en el archivo de configuración, deberás reiniciar el servicio de Home Assistant para que se apliquen los cambios. Puedes hacerlo desde el intérprete de comandos con “sudo service homeassistant restart”, o desde la interfaz web de HA, haciendo clic en el icono de la parte superior izquierda, seleccionando el icono de "Configuración" y llamando a la opción "Restart" de la sección "Server Management". El video http://bit.ly/2sAmD3F muestra algunos consejos que deberías tener en cuenta a la hora de editar la configuración.
Si tienes la intención de usar HA desde fuera de la LAN (por ejemplo, desde Internet), tiene varias opciones. Una de ellas es habilitar la compatibilidad con HTTPS y redireccionar el puerto 8123 en tu router. Esto te proporciona encriptación, pero expone tu instalación a Internet (y puede haber vulnerabilidades que permitan a posibles atacantes tomar el control de tu sistema/LAN). Una segunda opción (que es la que yo prefiero) es configurar una VPN en tu router (o incluso en tu ODROID) que te permita conectarte y acceder a HA (y a otros recursos LAN) de forma segura.
Si quieres utilizar HTTPS, para que tengas disponible todas la funciones, necesitas certificados SSL válidos (no autofirmados). Para obtener certificados válidos, deberás tener un nombre DNS público (por ejemplo, utilizar un servicio DNS dinámico como duckdns.org) y usar letsencrypt.org para configurar un certificado SSL válido para tu instalación. Los detalles paso a paso los puedes encontrar en el video http://bit.ly/2tY6LGb. Si necesitas utilizar certificados autofirmados, hay una guía disponible en http://bit.ly/2t0ObzH.
Independientemente del mecanismo de acceso (http o https), querrás configurar una contraseña. HA no es compatible con múltiples cuentas de usuario, pero puedes fijar una contraseña API que necesitarás para iniciar sesión en la interfaz web. La mejor forma de hacerlo es creando un archivo que almacene todos tus datos confidenciales (como contraseñas y URL), asígnale el nombre "secrets.yaml" y haz referencia a él dentro del archivo configuration.yaml.
$ cat /home/homeassistant/.homeassistant/secrets.yaml api_password: odroid $ cat /home/homeassistant/.homeassistant/configuration.yaml … http: api_password: !secret api_password …Ahora, cuando reinicies HA, se te pedirá una contraseña. Puedes encontrar más detalles sobre este tema en http://bit.ly/2rLGEkV.
Para conocer cómo funciona la configuración de HA, vamos a instalar algunos componentes. Voy a configurar el tiempo, algunas cámaras IP, Kodi y MPD, detección de presencia basada en WiFi y también un sensor de temperatura 1-wire conectado al ODROID.
El tiempo desde Darksky
Existen multitud de proveedores de información meteorológica ya integrados en HA (http://bit.ly/2t4l1Rh), para que puedas elegir tu favorito. Me quedo con DarkSky (http://bit.ly/2t4gq0S), que proporciona pronósticos bastante precisos de mi zona. Deberías consultar la página de ayuda del componente para conocer los detalles de su configuración y qué variables son las que puedes utilizar. Tendrás que registrarse en Dark Sky y obtener una clave API que te permitirá hacer 1000 peticiones al día de forma gratuita. Lo mejor es guardar esta clave API dentro de tu archivo secrets.yaml (reemplaza con tu propia clave):
darksky_api_key: 87f15cbb811204412cc75109777ea5cfLa configuración tiene varias variables, la mayoría de las cuales son opcionales, sin embargo, en configuration.yaml, debajo de la sección sensor deberías tener lo siguiente (tomate la libertad de eliminar la entrada "platform: yr"):
sensor: - platform: darksky api_key: !secret darksky_api_key name: Dark Sky monitored_conditions: - summary - precip_type - precip_probability - temperature - humidity - precip_intensity - wind_speed - pressure - wind_bearing - apparent_temperature - icon - minutely_summary - hourly_summary - temperature_max - temperature_min units: si update_interval: '00:15'El código es en su gran mayoría autoexplicativo. Éste configura una nueva plataforma del tipo "darksky", con un nombre específico (opcional) y una api_key (obligatoria), y extrae un conjunto de parámetros (monitored_conditions) desde proveedor de información meteorológica cada 15 minutos. Tu ubicación exacta se toma de los parámetros de latitud/longitud en Home Assistant, de modo que debes asegurarte de que sean correcta. Tras reiniciar el servicio homeassistant, deberías poder ver las variables monitorizadas en forma de insignias en la parte superior de la ventana. Al hacer clic en alguna, te mostrara cómo ese valor en particular ha cambiado con el tiempo.
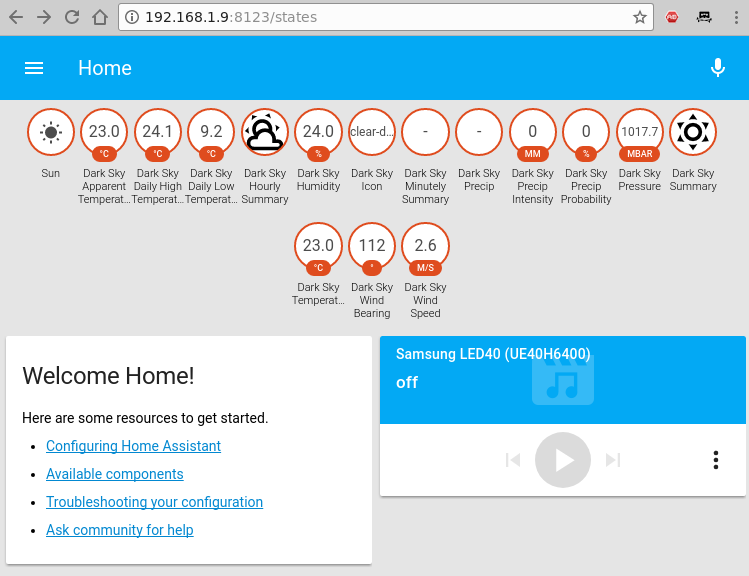
Visualización de cámaras IP
HA soporta muchas cámaras (http://bit.ly/2t4DtsD),incluida la interpretación de datos desde un archivo, que podría utilizarse para presentar un gráfico, o datos visuales generados por otras herramientas. Usaremos el componente Generic MJPG Camera (http://bit.ly/2t4tIKM) y el componente Local File (http://bit.ly/2s4Y5w4)º.
La cámara que queremos monitorizar está disponible en http://bit.ly/2t4cHkc (es una webcam pública), que debemos añadir al archivo secrets.yaml.
camera1_stream_url: http://iris.not.iac.es/axis-cgi/mjpg/video.cgi?resolution=320x240 camera1_still_url: http://iris.not.iac.es/jpg/image.jpgLa parte de la configuración dentro de configuration.yaml debería parecerse a esto para ambos sistemas de cámara:
camera: - platform: mjpeg mjpeg_url: !secret camera1_stream_url still_image_url: !secret camera1_still_url name: Observatory in Spain - platform: local_file file_path: /tmp/tux.jpgComo de costumbre, deberás reiniciar el servicio de HA para volver a leer la configuración (este también podría ser un buen momento para comentar el componente de "introducción"). Tenga en cuenta que cuando haces clic en una webcam, verás una transmisión en vivo, de lo contrario, la imagen fija se actualiza cada 10 segundos.
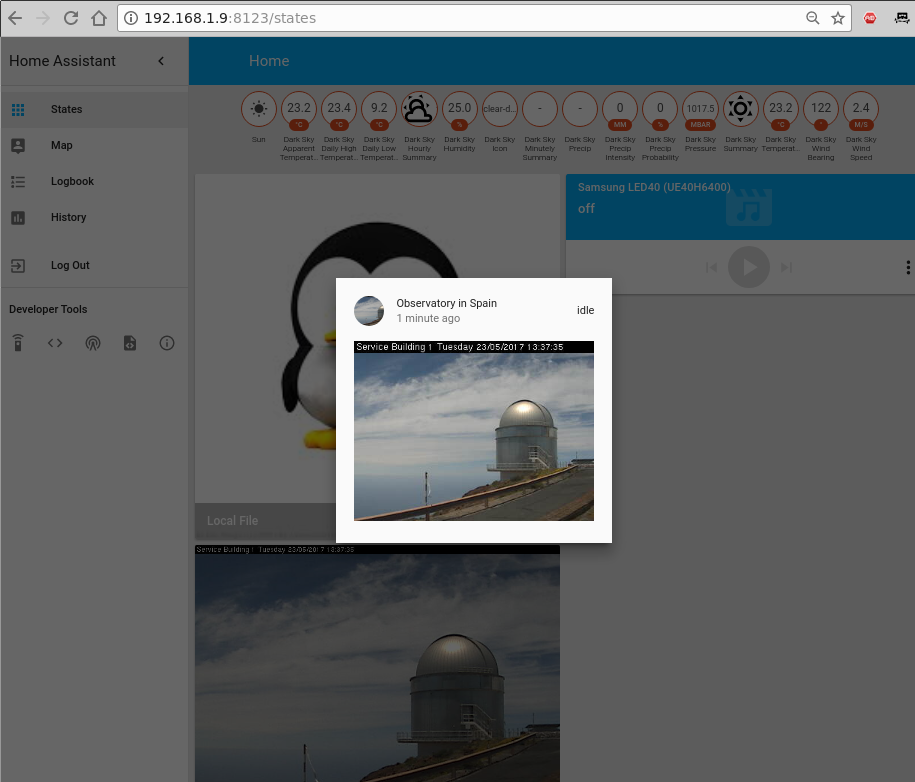
Entonces, ¿Qué podemos hacer con estas webcams configuradas aparte de mirarlas? Bueno, puede usarlas con otros componentes como OpenCV (http://bit.ly/2s4UUEJ) para generar “activadores” (señales que acciones un determinado proceso) cuando se vean determinados rostros, o Seven Segments Display (http://bit.ly/2sAbOP0), que permite tomar lecturas de varias pantallas digitales.
Kodi y MPD
Para configurar reproductores multimedia, puedes buscar en la lista de componentes Media Player en http://bit.ly/2s0IAtQ. Para configurar Kodi (http://bit.ly/2sA5qr6),deberás activar la opción "Allow remote control via HTTP" (http://bit.ly/2t4cYne) y configurar primero el correspondiente nombre de usuario y contraseña. Para hacerlo, añade el usuario y la contraseña al archivo secrets.yaml:
kodi_user: kodi kodi_pass: kodiA continuación, edita configuration.yaml:
media_player: - platform: kodi host: 192.168.1.140 name: Kodi Livingroom username: !secret kodi_user password: !secret kodi_passPara configurar MPD, suponiendo que ya tienes un servidor MPD en tu red, agrega el componente MPD (http://bit.ly/2s5sbzE) y añade la contraseña a secrets.yaml:
mpd_secret: mpdY después, edita configuration.yaml:
media_player: ... - platform: mpd host: 192.168.1.140 name: MPD Living password: !secret mpd_secretTras reiniciar Home Assistant, aparecerán los dos nuevos reproductores multimedia y podrá ver su estado (reproducción/detención), controlar el volumen e incluso cambiar la lista de reproducción actual o usar el componente de conversión texto-voz para que el reproductor multimedia "pronuncie" lo que quieras.
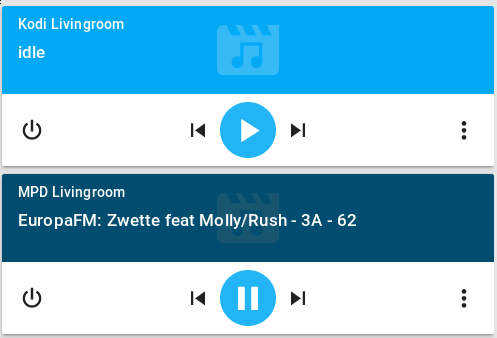
Detección de presencia
Los componentes de detección de presencia (http://bit.ly/2t0Gt8H) intentan rastrear las ubicaciones de las personas para que puedas aplicar reglas de geofencing (por ejemplo, hacer algo si una persona entra o sale de una ubicación). Por lo general, el seguimiento se realiza mediante la detección de dispositivos conectados a un router (a través de wifi), mediante la proximidad del bluetooth (http://bit.ly/2s0Sqfw) o haciendo uso de servicios de ubicación como Owntracks (http://bit.ly/2rLQdR1).
Usaremos un rastreador basado en routers que, dependiendo de tu router, se conecta periódicamente a la interfaz de gestión de tu router, lista la tabla ARP y descubre qué dispositivos están conectados. Son muchos los tipos de routers soportados, desde despóticos de gama alta como Cisco, hasta router de consumo como Asus, Netgear y TP-Link. Incluso son compatibles los firmwares de código abierto, como OpenWRT, DD-WRT y Tomato.
Utilizaremos un router Asus con SSH habilitado, de modo que necesitamos el componente ASUSWRT: http://bit.ly/2s4T32Q. Puedes elegir entre iniciar sesión con nombre de usuario/contraseña o configurar una clave SSH e iniciar sesión. Ten en cuenta que determinadas versiones del firmware cuentan con ciertas medidas de seguridad que limitan la cantidad de conexiones SSH y pueden incluir tu IP en una lista negra si se hacen muchas conexiones.
Como de costumbre, colocaremos los datos sensibles (como la ruta a la clave o la contraseña ssh) dentro del archivo secrets.yaml:
router_user: admin router_password: my_secret_passwordDentro de configuration.yaml añade la siguiente sección:
device_tracker: - platform: asuswrt host: 192.168.1.1 username: !secret router_user password: !secret router_password interval_seconds: 120 consider_home: 300 track_new_devices: yesLa página de configuración del rastreador del dispositivo (http://bit.ly/2s4WPcA) proporciona más detalles sobre las opciones que puede usar. La opción interval_seconds es el tiempo entre lecturas (2 minutos) y la opción consider_home lo mantiene "en home" incluso si tus dispositivos no aparecen durante 300 segundos.
Una vez que reinicies HA y después de realizar la primera busqueda exitosa, se creará un nuevo archivo, llamado known_devices.yaml. Aquí podrás asignar un nombre amigable e incluso una imagen a un dispositivo específico, o hacer que otros dispositivos sean ignorados.
Una entrada en known_devices.yaml debería verse así:
aldebaran: hide_if_away: false mac: 00:1E:06:31:8C:5B name: aldebaran picture: /local/aldebaran.png track: true vendor: WIBRAINTen en cuenta que ha añadido una ruta a la imagen local que se almacena en /home/homeassistant/.homeassistant/www/aldebaran.png. Puedes crear la carpeta "www" con el siguiente comando:
$ sudo mkdir /home/homeassistant/.homeassistant/wwwSi hay dispositivos que no deseas monitorizar, puede fijar "track: false" en el archivo known_devices.yaml.

Medición de la temperatura
Una característica muy potente de Home Assistant es la capacidad de rastrear todo tipo de sensores (http://bit.ly/2cNb4gJ). Queremos monitorizar un sensor de temperatura basado en el protocolo 1-Wire, conectado localmente al ODROID (http://bit.ly/2s12ZPx). Antes de agregar el sensor a HA, asegúrate de que sea legible desde la línea de comando. Puedes recurrir a la guía de configuración de la wiki en http://bit.ly/2s0zbTp.
Necesitaras conocer el ID del sensor para añadirlo a HA:
$ ls /sys/bus/w1/devices/ 28-0516866e14ff w1_bus_master1 $ cat /sys/bus/w1/devices/28-0516866e14ff/w1_slave 92 01 4b 46 7f ff 0c 10 b5 : crc=b5 YES 92 01 4b 46 7f ff 0c 10 b5 t=25125A continuación, realiza los siguientes cambios en configuration.yaml y sondea el sensor cada 5 minutos:
sensor: ... - platform: onewire names: 28-0516866e14ff: Living room scan_interval: '00:05'Tras reiniciar HA, la nueva lectura será visible en la interfaz web a modo de insignia en la parte superior de la página.
Ordenando las vistas
Observarás que una vez que empiezas a añadir componentes, la interfaz web se muestra algo desordenada con gran cantidad de elementos dispersos por todas partes. Puedes usar grupos y vistas para limpiar la interfaz y ubicar los elementos relacionados en tus propias pestañas. Para entender todo esto, vamos a tirar un poco de vocabulario.
Las “Entities” (Entidades) son variables que proporcionan datos, como un sensor o interruptor. Las plataformas (como dark_sky) generalmente proporcionan acceso a múltiples entidades (temperaturas mínimas/máximas o pronóstico). Puede ver una lista de entidades, sus nombres y su valor si navega en la interfaz web por Developer tools -> States (<>) -> Entities.
Un “group” (grupo) es simplemente un objeto que contiene una lista de entidades. Visualmente, un grupo se presenta como un panel o una ficha. Por defecto, existe el grupo "group.all_devices" que almacena los elementos descubiertos por una plataforma de rastreo de dispositivos. Los grupos generalmente contienen una lista de entidades.
Una “view” (vista) se presenta como una pestaña separada dentro de Home Assistant. Las vistas son en realidad grupos de grupos y se diferencian de los grupos normales por tener la propiedad "view: yes". También puedes añadir a una vista entidades individuales, así como grupos.
Agruparemos nuestros sensores existentes en las siguientes categorías:
- hLa primera pestaña es Home y contiene los siguientes grupos (denominada internamente default_view, de modo que aparece cuando inicias sesión):
- Datos meteorológicos
- Información de presencia
- Información del sistema (para mostrarte si hay actualizaciones disponibles)
- La segunda pestaña se llamará Media y contiene los siguientes grupos:
- Reproductores multimedia
- La pestaña final se llamará Images y contiene:
- Webcams
La configuración debería parecerse a la siguiente lista
group: default_view: view: yes entities: - group.weather - group.presence - group.systeminfo media: view: yes entities: - group.mediaplayers images: view: yes entities: - camera.observatory_in_spain - camera.local_file weather: name: Weather entities: - sensor.dark_sky_apparent_temperature - sensor.dark_sky_daily_high_temperature - sensor.dark_sky_daily_low_temperature - sensor.dark_sky_hourly_summary - sensor.living_room presence: name: Presence entities: - device_tracker.aldebaran - device_tracker.nutty systeminfo: name: System Info entities: - updater.updater mediaplayers: name: Media Players entities: - media_player.mpd_livingroom - media_player.kodi_livingroom
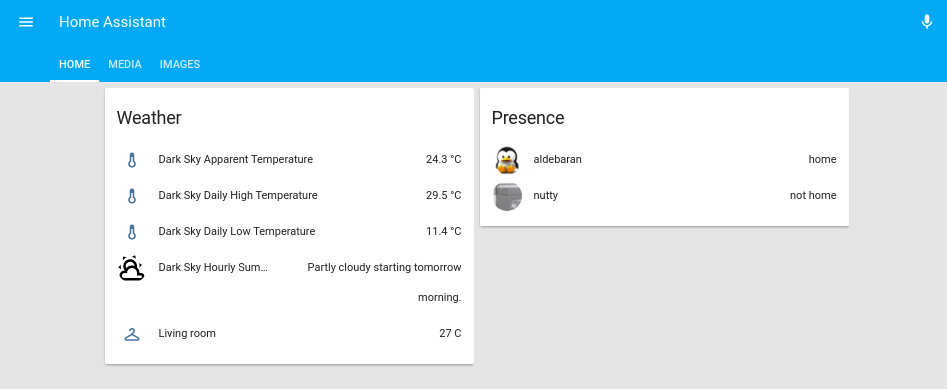
Tienes disponible más detalles sobre los grupos y la distribución en el video de http://bit.ly/2s5d6xT.
Actualizaciones
Como Home Assistant no ha sido instalado a través de apt-get, deberás gestionar manualmente las actualizaciones. Antes de actualizar, es conveniente leer las notas de la versión y verificar que la actualización no dañe la configuración creada, ya que a veces se suele rediseñar la configuración de los nuevos componentes, lo que significa que tendrías que volver a hacerla. Puede obtener notificaciones de nuevas versión utilizando la entidad updater.Updater, que comprueba periódicamente si hay versiones nuevas y puede mostrarlas en Home Assistant. Las actualizaciones son bastante frecuentes, y puede aparecer una versión principal cada 2-3 semanas. El procedimiento de actualización es simple, y los detalles los puedes encontrar en http://bit.ly/2s0Kn24.
$ sudo service homeassistant stop $ sudo su -s /bin/bash homeassistant $ source /srv/homeassistant/bin/activate (homeassistant)$ pip3 install --upgrade homeassistant (homeassistant)$ exit $ sudo service homeassistant startEn artículos posteriores, analizaremos la configuración de algunos componentes más complejos, como un relé remoto o una unidad de aire acondicionado, configuraremos automatizaciones y montaremos un cuadro de mandos. Para comentarios, preguntas y sugerencias, visita el hilo de soporte en http://bit.ly/2s13GbB.
































































 ¿Cómo empezaste con los ordenadores?
Cuando tenía 6 años, me topé con mi primer ordenador. Cuando visitaba a mi tía, mi primo tenía algunos ordenares 386. Como muchos otros, El ordenador era una consola de juegos para mí. Jugaba a Sango Fighter, Prince Of Persia, Prehistorik, Jazz Jackrabbit y a mucho otros. Empecé a estudiar seriamente los sistemas informáticos avanzados tras realizar el servicio militar, porque quería hacer mi propio sistema operativo. Estudié muchos aspectos de los ordenadores, aunque mi materia favorita era el software integrado. Quería hacer una obra maestra de un producto como es un sistema integrado al completo.
¿Cómo empezaste con los ordenadores?
Cuando tenía 6 años, me topé con mi primer ordenador. Cuando visitaba a mi tía, mi primo tenía algunos ordenares 386. Como muchos otros, El ordenador era una consola de juegos para mí. Jugaba a Sango Fighter, Prince Of Persia, Prehistorik, Jazz Jackrabbit y a mucho otros. Empecé a estudiar seriamente los sistemas informáticos avanzados tras realizar el servicio militar, porque quería hacer mi propio sistema operativo. Estudié muchos aspectos de los ordenadores, aunque mi materia favorita era el software integrado. Quería hacer una obra maestra de un producto como es un sistema integrado al completo.

